DSMC and PICMC documentation
2022-02-17
1.1 Numerical Constraints
In Direct Simulation Monte Carlo (DSMC) simulation, the transport of particles along their trajectories can be considered as a grid less simulation method. The main function of the simulation grid in space is to resolve the collision dynamics, namely the dimension of the grid cells define the neighbourhood of particles which can collide with each other during a time step. Thus, in DSMC simulation the main criterion to select the cell spacing is the mean free path \(\lambda\).
In Particle-in-Cell Monte-Carlo (PIC-MC) plasma simulation, an additional function of the volume grid is to discretize the electric and magnetic field. The grid spacing should be appropriate to resolve gradients in the electric potential. This is most critical at the plasma sheath and in regions of high plasma density. The crucial criterion for cell spacing in plasma simulation is the Debye length \(\lambda_D\), which is a characteristic shielding length of potential fluctuations in the plasma.
1.1.1 Numerical constraints in Direct Simulation Monte Carlo (DSMC)
For a gas flow simulation, the set up of the simulation domain and the particle statistics requires to decide values for certain parameters, which are listed in the following. For simplicity we assume that all cells have a cubical shape. Then, the following parameters are relevant
- \(a\) = Cell dimension (m)
- \(V_c\) = Cell volume = \(a^3\)
- \(N_{\textrm{Real}}\) = Quotient between physical number of particles \(N\) and number of simulation particles \(N_S\)
- \(\delta t\) = Period of one time cycle.
The first step is to estimate the mean free path \(\lambda\) from the gas species and the expected pressure range.
The mean free path \(\lambda\) is defined as the mean travelling distance of a particle between two collisions. If a particle ensemble has a Maxwellian velocity distribution, it can be computed via
\[\lambda = \dfrac{1}{\sqrt{2}\,n\,\sigma} = \dfrac{k_\textrm{B}\,T}{\sqrt{2}\pi\,d^2\,p}\](1.1)
with the following parameters
- \(n\) = Density
- \(p\) = Pressure
- \(k_B\) = Boltzmann constant
- \(d\) = Effective collision diamater of the gas particle
- \(T\) = Temperature
- \(\sigma\) = Effective collision cross section
Eqn. (1.1) shows, that \(\lambda\) is inversely proportional to the total pressure. From Pfeiffer-Vacuum / Mean free path the following numerical values are obtained for a few common gases at \(T\)=0 °C.
| Species | \(p\times\lambda\) (Pa mm) | Atomic diameter (nm) |
|---|---|---|
| Ar | 6.34 | 0.382 |
| H2 | 11.06 | 0.288 |
| N2 | 5.96 | 0.394 |
| O2 | 6.41 | 0.380 |
For temperatures \(T\) different than \(0\,^\circ C\) or \(273.15 K\), the mean free path can be obtained from Table 1.1 by multiplying with \(T (K)/273.15\). The cell dimension \(a\) should be less than the mean free path to maintain proper collision statistics,
\[ a \le \lambda\]
Once, the cell dimension \(a\) is chosen, the maximum allowable timestep \(\delta t_{max}\) can be computed from the mean thermal velocity \(\overline{c}\) of the gas species,
\[\overline{c} = \sqrt{\frac{8 kT}{m\pi}}\](1.2) \[\delta t_{max} = \frac{a}{\overline{c}}\](1.3)
Finally, the physical number \(N_c\) of particles in a cell with volume \(V_c\) follows from the ideal gas equation,
\[N_c = \frac{p V_c}{k T}\](1.4)
The number \(N_S\) of simulated particles is usually much lower than the physical number of particles. It can be chosen as a compromise between statistical accuracy and computational speed. A good range for \(N_S\) is from 10 till 100 or more particles in regions of maximum density. In regions, where almost no collision is to be expected, \(N_S\) can be also chosen as less than 10 or even less than 2. If an average particle number per cell \(N_c\) is obtained from Eqn. (1.4), and \(N_S\) is the desired mean simulation particle number per cell, the statistical weight factor can be obtained via
\[N_{\textrm{Real}} = \frac{N_c}{N_S}\](1.5)
1.1.2 Numerical example for DSMC
In this numerical example, we are assuming to have Argon gas at a temperature of 300 K and a total pressure of \(0.5\,\textrm{Pa}\). From Table 1.1 and Eqn. (1.1) follows a mean free path of
\[\lambda_{\textrm{Ar, 300 K}} = 6.34\,(\textrm{Pa mm})\times\frac{300 K}{273.15 K\times 0.5 Pa} = 13.94\,\textrm{mm}\]
That means that the maximal cell spacing can be almost 14 mm; in order to be on the safe side and have a convenient factor between cells and space, we chose \(a = 10\,\textrm{mm}\), leading to a cell volume of \(V_c = a^3 = 10^{-6}\,\textrm{m}^3\). From Eqn. (1.2) we get \(\overline{c} = 398.5\,\textrm{m/s}\) as mean thermal velocity, which - via Eqn. (1.3) - defines an upper limit of the time step of \(\delta t_{max} = 2.5\times 10^{-5}\,\textrm{s}\).
For the particle scaling factor \(N_{\textrm{Real}}\) we consider that we would like to have a mean simulation particle number per cell of \(N_S = 20\). From Eqn. (1.4) the physical particle number per cell computes to \(N_c = 1.21\times 10^{14}\). Via Eqn. (1.5), this translates to \(N_{\textrm{Real}} = 6.05\times 10^{12}\).
1.1.3 Numerical constraints in Particle-in-Cell Monte-Carlo (PIC-MC) simulation
1.1.3.1 Cell spacing
One limitation for the maximum time step width is given due to the implemented Monte Carlo algorithm. According to their velocities particles must stay within a grid cell for at least on time step. Otherwise the collision probabilities are not evaluated correctly, i.e. a cell hopping occurs. Hence, the product of time step and particle velocity must not exeed the cell spacing,
\[\Delta t \times v < \Delta s\](1.6)
The velocity of charged particles can be estimated from the maximum voltage in the simulation setup. If neglecting the energy loss due to inelastic collisions, the voltage potential is applied as kinetic energy to the charged particle:
\[\frac{m\,v^2}{2\,q} = E_\textrm{kin} (\textrm{eV}) = U_\textrm{max} (\textrm{V}) \Rightarrow v = \sqrt{\frac{2\,U\,q}{m}} \left[\dfrac{\textrm{m}}{\textrm{s}}\right]\](1.7)
with \(q = 1.60211 \times 10^-19\) (As). The table below lists electron velocities for various energies and the accordant distance covered at a time step width of \(\delta t=10^{-11}\) (s):
| Energy (eV) | \(v_{\textrm{Electron}}\) (m/s) | \(v_{\textrm{Electron}}\delta t\) (\(\mu\)m) |
|---|---|---|
| 100 | \(5.932 \times 10^6\) | 59.32 |
| 200 | \(8.389 \times 10^6\) | 83.89 |
| 300 | \(1.027 \times 10^7\) | 102.7 |
| 400 | \(1.186 \times 10^7\) | 118.6 |
| 500 | \(1.326 \times 10^7\) | 132.6 |
1.1.3.2 Collision frequency
According to the Wikipedia1 the collision frequency \(nu\) can be descibed as the rate of collisions between two species in an given volume and time. Regarding both species \(A\) and \(B\) as hard spheres, \(nu\) is expressed as
\[\nu = n_A n_B \sigma_{AB} \sqrt{\frac{8 k_B T}{\mu_{AB}\pi}}\,(m^{-3} s^{-1})\](1.8)
where
- \(n_A\,(m^{-3})\) is the number density of species \(A\)
- \(n_B\,(m^{-3})\) is the number density of species \(B\)
- \(\sigma_{AB}\,(m^2)\) is the collision cross section of \(A\) and \(B\)
- \(k_B\, (m^2\,kg\,s^{-2}\,K^{-1})\) is the Boltzmann’s constant
- \(T\,(K)\) is the temperature
- \(\mu_{AB}\,(kg)\) is the reduced mass of A and B
Since we are interested in the lower bound of the time step, only the highest cross section is of interest which is usually the reaction of the main gas species with itself.
1.1.3.3 Electron collision frequency
The collision frequency for neutrals in an ideal gas can be estimated from
\[\nu = N\,\pi d^2\sqrt{\frac{8 k_B T}{m \pi}}\](1.9)
Whereas \(N\) is the number density, \(d\) the effective atom radius, \(k_B\) the Boltzmann constant, \(T\) the gas temperature and \(m\) the molecular mass. Transfered to the electron collision frequency in a partly ionized plasma one could use the above estimation with:
- \(\pi d^2 \rightarrow \sigma\) = the electron-neutral collision cross section with the primary gas species
- \(T \rightarrow T_e\) = the electron temperature whereas 1 eV = 11604.5 K
- \(m \rightarrow m_e\) = the electron rest mass of \(9.1091 \times 10^{-31}\) kg
Thus, for a H2-plasma with TH2 = 500 K, Te = 5 eV and an approximated \(\sigma\) = 10-19 m2 one gets:
- \(\lambda=1.0838\times 10^{10}\,\textrm{Hz at }P_{H_2} = 500\,\textrm{Pa}\)
- \(\lambda=2.1677\times 10^{10}\,\textrm{Hz at }P_{H_2} = 1000\,\textrm{Pa}\)
- \(\lambda=4.3355\times 10^{10}\,\textrm{Hz at }P_{H_2} = 2000\,\textrm{Pa}\)
For a valid simulation, time step width must be well below the reciprocal of the collision frequency.
1.1.3.4 Plasma frequency
The plasma frequency \(\omega_p\) is the angular frequency of the electron oscillations around the ions. It depends only on electron mass and density:
\[\omega_p = \sqrt{\frac{n e^2}{\epsilon_0 m_e}}\](1.10)
- \(n\) = Electron density
- \(e\) = Electron charge (\(1.6021\times 10^{-19}\) As)
- \(\epsilon_0\) = Dielectric permittivity (\(8.8542\times 10^{-12}\) F/m)
- \(m_e\) = Electron mass (\(9.1091\times 10^{-31}\) kg)
In order to properly resolve the plasma oscillations, the electron time step should be well below the respective oscillation period e.g., \(\delta t < 0.1 \omega_p\), as can be estimated from the following table:
| Electron density [m-3] | Plasma frequency [s-1] | Oscillation period [s] |
|---|---|---|
| 1015 | \(1.78\times 10^{9}\) | \(5.605\times 10^{-10}\) |
| 1017 | \(1.78\times 10^{10}\) | \(5.605\times 10^{-11}\) |
| 1019 | \(1.78\times 10^{11}\) | \(5.605\times 10^{-12}\) |
1.1.3.5 Debye length
The Debye length \(L_D\) describes the electrical shielding capability of the plasma. The potential difference induced by a local excess charge will drop to \(1/e\) of the original potential at the distance of \(L_D\). For electrons, the Debye length is given by:
\[L_D = \sqrt{\frac{\epsilon_0 k_B T_e}{n_e e^2}} \simeq 69.01\times\sqrt{\frac{T_e}{n_e}} \simeq 6070\times\sqrt{\frac{E (\textrm{eV})}{n_e}}\]
Here, \(\epsilon_0\) is the vacuum permittivity, \(k_B\) the Boltzmann constant, \(T_e\) the electron temperature, \(n_e\) the electron density and \(e\) the electron charge.
In order to properly resolve the electric potential distribution in the simulation grid, the cell size has to in the same order of magnitude as the Debye length. From (Langdon 1970) follows, that the cell spacing shall be less than \(\pi L_D\). In (Tskhakaya et al. 2007) a constraint of:
\[\delta_x \le 3.4 L_D\]
is suggested. This is what we also adopted in our constraint check message for the Debye length on plasma simulation startup. If this constraint is broken, artificial numerical oscillations will take over leading to “artificial heating,” i.e. more energy will be gained in the plasma than actually put into the system via the electrodes, and the simulation will become unstable.
Our simulation tool cannot predict the plasma density of any given simulation case. Therefore, we give some estimations for typical cases:
- We assume 5 eV for electrons as this is a very typical electron temperature in magnetron sputtering discharges.
- A plasma density of 1017/m³ corresponds to an experimentally realistic density (still with moderate power density, e.g. 50-100 W for a 3 inch cathode).
- A plasma density of less than 1015/m3 is what we often have in simulation (especially 3D) as feasible compromise between realistic power density and computation time.
As an example, for \(n_e = 10^15 m^{-3}\) and \(T_e = 5 eV\), the constraint \(3.4 L_D\) is computed to 1.459 mm.
If the simulation output shows “Failure” at the Debye length check this is merely an informative message based on the assumed plasma density of 1015/m³ or 1017/m³ and electron temperature of 5 eV. If the actual simulation setup is different from that it may be still numerically valid. If in doubt it helps to check if two simulation runs with slightly changed cell spacing yield the same overall results.
1.1.3.6 Gyrokinetics
The implemented leap-frog algorithm from Boris is very robust at comparatively small computation costs. Nevertheless if the chosen time step witdh is too large, gyrokinetic trajectories could not be resolved sufficiently as seen in the pictures below. For a proper estimation use the following equation:
\[R_{\textrm{Larmor}} = \frac{m_e\left|\vec{v}\right|}{q_e\left|\vec{B}\right|}\](1.11)
with
- \(m_e = 9.1091\times 10^{-31}\) kg
- \(q_e = 1.6021\times 10^{-19}\) As
Eqn. (1.11) yields the path radius of an electron at constant velocity \(v\) perpendicular to a homogenous magnetic field \(B\). We still lack informations on how the time step related granularity is influencing the plasma simulation and the results respectively. However, for a proper simulation of gyrokinetic plasmas it should not exeed a certain limit. Apparant from the pictures below, at magnetic field strengths around 100 mT and electron velocities around \(5\times 10^6\) m/s, the time step for electrons should not exeed 10-10 s. These values are commonly valid for magnetron discharges in PVD sputtering processes, on which the PICMC simulation environment is focused on.
| Time Step = 10-11 [s] | Time step = 10-10 [s] |
|---|---|
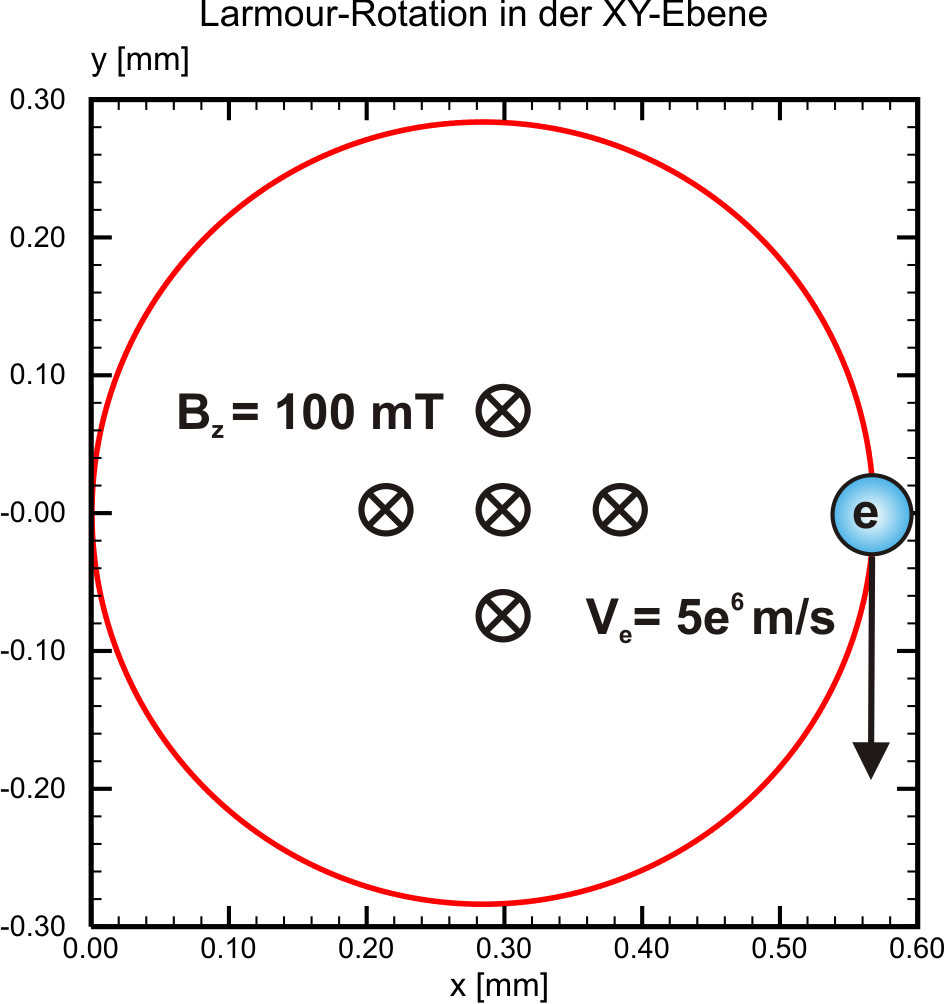 |
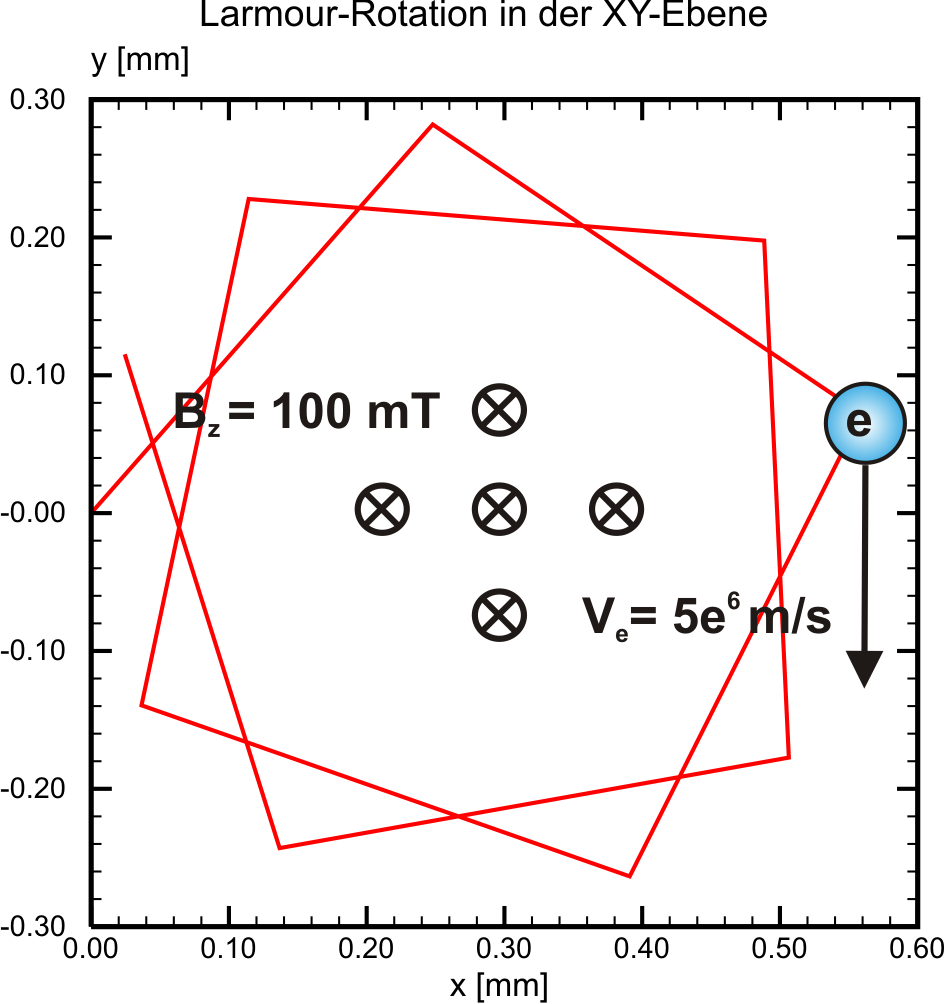 |
1.1.3.7 Isotropic vs. anisotropic cell spacing
Within the Particle-in-Cell (PIC) algorithm charged particles are mapped on the cell nodes by a weighting scheme. Then, in a successive computation step the Poisson Equation of the electric field can be solved consistently to the weighted charge distribution. The PIC weighting scheme in general delocalized a point charge to a finite sized space charge with an appropriate shape function. The charge on a certain node is then given by the fraction of the space charge within the cell volume.
In a homogenous grid the particle shape is equivalent to the cell spacing at every point. Thus, for a bilinear (trilinear) weighting scheme, the charge on a certain cell node can be described as the convolution of two square pulses over time:
\[Q_{Node}(t) = f_{Charge}(x,t)f_{Node}(x) = \int dx\, \Pi_{\Delta x}(x-v_x t)\Pi_{\Delta x}\]
The resulting plot for this mathematical operation can be seen below. Now if the particle's speed \(v_x\) is increased or the cell width \(\Delta x\) is decreased, the variation of \(Q(x,t)\) over time increases:
\[\left.\frac{Q(t)}{dt}\right|_{(v_x, \Delta x)} < \left.\frac{Q(t)}{dt}\right|_{2v_x, \Delta x}\,\,\textrm{and}\,\,\left.\frac{Q(t)}{dt}\right|_{(v_x, 2 \Delta x)} < \left.\frac{Q(t)}{dt}\right|_{v_x, \Delta x}\]
If the charge on a nodes varies over time so does the electric field resulting from the solution of the poisson equation:
\[\frac{Q(t)}{dt}\approx \frac{E(t)}{dt}\]