DSMC and PICMC documentation
2024-09-20
2 Physical background
2.1 Units and conversion factors
This chapter deals with typical quantities and units, that are relevant in Direct Simulation Monte Carlo (DSMC) - gas flow simulation and Particle-in-Cell Monte-Carlo (PIC-MC) - plasma simulation.
2.1.1 Particle flow rate (sccm) and current (A)
In vacuum technology, particle flows are often measured in sccm, which stands for standard cubic centimeters per minute. This is actually proportional to the number of gas molecules per time unit and thus, it is a very convenient unit for kinetic simulation methods based on particles. The term standard conditions stands for atmospheric pressure on earth at a temperature of \(0\,^\circ\)C:
Pressure \(p = 1.01325 \textrm{bar} = 1.01325\times 10^5\,\textrm{Pa}\)
Temperature \(T = 0\,^\circ\textrm{C} = 273.15\,\textrm{K}\)
Volume \(V = 1\,\textrm{cm}^3 = 10^{-6}\,\textrm{m}^3\)
The number \(N\) of particles within a given volume \(V\) can be obtained from the ideal gas equation ((eq:ideal_gas?)).
\[N = \frac{pV}{k_B T}\]{#eq:ideal_gas}
With the Boltzmann constant \(k_B=1.38065\times 10^{-23}\,\textrm{J/K}\) and a volume of \(V = 1\,\textrm{cm}^3\) we obtain \(N=2.68675\times 10^{19}\). Since sccm is the flow rate given per minute but we would like to have the number of particles per second, we have to divide \(N\) by 60. This yields the number particles per second for 1 sccm as given in Eqn. ((eq:sccm_particles?)).
\[1\,\textrm{sccm} \approx 4.47796\times 10^{17}\,\textrm{s}^{-1}\]{#eq:sccm_particles}
From the electron charge \(e = 1.60218\times 10^{-19}\,\textrm{(As)}\) follows, that one ampere corresponds to a number of \(6.24150\times 10^{18}\) particles (electrons or ions) per second. A comparison with the particle flow rate in Eqn. ((eq:sccm_particles?)) yields the conversion factor between A and sccm.
\[1\,\textrm{A} \approx 13.9397\,\textrm{sccm}\]{#eq:conversion_A_sccm}
2.1.2 Pumping speed
The volumetric pumping speed \(S_p\) is defined as pumped gas volume / time. In case of an orifice with area \(A\) and ideal pumping behavior, the maximum possible pumping speed \(S_{p.max}\) is
\[S_{p.max} = \frac{\overline{c}}{4}\times A\]{#eq:pumping_speed_orifice}
In Eqn. ((eq:pumping_speed_orifice?)), \(A\) is the area of the pumping orifice, and \(\overline{c}\) is the mean thermal speed of a gas molecule, which follows from Eqn. ((eq:mean_thermal_speed?)).
\[\overline{c} = \sqrt{\frac{8 kT}{m\pi}} \simeq 145.5\textrm{ (m/s)} \times\sqrt{\frac{T\textrm{ (K)}}{m\textrm{ (u)}}}\]{#eq:mean_thermal_speed}
At a temperature of 300 K, the following mean thermal speeds are obtained for a variety of gases:
| Species | Relative mass (u) | Mean thermal velocity \(\overline{c}\) (m/s) |
|---|---|---|
| Kr | 83.8 | 275 |
| Ar | 39.9 | 399 |
| O2 | 32.0 | 446 |
| SiH4 | 32.1 | 445 |
| N2 | 28.0 | 476 |
| H2 | 2.02 | 1770 |
| H | 1.01 | 2510 |
2.1.3 How to specify the transmission factor for a surface with given pumping speed
Pumping surfaces in DSMC- or PIC-MC-simulation are characterized by an absorption factor \(f\in [0\ldots 1]\), while the volumetric pumping speed \(S_p\) is given as an external input (e.g. the nominal pumping speed of an attached turbomolecular pump). In such cases, the pump factor is selected as the ratio between given pumping speed \(S_p\) and maximum possible pumping speed \(S_{p.max}\) from Eqn. ((eq:pumping_speed_orifice?)).
\[f = \frac{S_p}{S_{p.max}} = \frac{4 S_p}{A\overline{c}}\]{#eq:pump_factor}
2.1.3.1 Numerical example
We assume that a turbomolecular pump with a nominal pumping speed of \(S_p = 1.0\) m3/s for Argon at 300 K is attached to a circular surface with a diameter of 133 mm. From that, the following steps are necessary to compute the effective pump factor \(f\):
The area \(A\) of the flange is \(\pi r^2\) with r=66.5 mm; thus, A = 0.01389 m2
From to Eqn. ((eq:mean_thermal_speed?)) follows that \(\overline{c} = 399\) m/s for Argon at 300 K
According to Eqn. ((eq:pumping_speed_orifice?)) the maximum possible pumping speed is 1.386 m3/s
From that, Eqn. ((eq:pump_factor?)) yields \(f = 72.16\)%
2.1.4 Relation between gas flow, pumping speed and pressure
Especially in DSMC simulation, it is helpful to estimate the mean equilibrium pressure, when the gas flow through the inlet and the pumping speed are given. This can be done based on the following consideration:
In equilibrium, the time derivative \(dN/dt\) of the total number of particles \(N\) in a chamber volume, which can be expressed as the balance between source and drain, is zero.
\[\frac{dN}{dt} = F_{in}f_{sccm} - S_p n = F_{in}f_{sccm} - S_p \frac{p}{kT} = 0\]{#eq:number_balance_tmp}
Here, \(F_{in}\) is the gas flow in sccm, \(f_{sccm}=4.47796\times 10^{17}\textrm{ (sccm}^{-1}\textrm{s}^{-1}\textrm{)}\) is the conversion factor from Eqn. ((eq:sccm_particles?)), \(S_p\) is the nominal pumping speed, and \(n=N/V\) is the number density of gas molecules. According to the ideal gas equation ((eq:ideal_gas?)), \(n\) can be written as \(p/kT\). Eqn. ((eq:number_balance_tmp?)) can be written as
\[p = \Phi\frac{F_{in}}{S_p};\,\,\Phi = kTf_{sccm}\]{#eq:pressure_flow_pumping}
The factor \(\Phi\) is independent from the gas species, typical values as a function of temperature are listed in Table ((tbl:factor_phi?)).
| Temperature (K) | \(\Phi\textrm{ (Nm/(sccm s))}\) |
|---|---|
| 300 | 0.001854 |
| 350 | 0.002163 |
| 400 | 0.002472 |
| 450 | 0.002781 |
| 500 | 0.003091 |
2.1.4.1 Numerical example
In a chamber with the turbomolecular pump described in Section (sec:num_example_sp?), Argon is injected with a flow rate of 500 sccm, and the mean gas temperature is 300 K. According to Eqn. ((eq:pressure_flow_pumping?)), the equilibrium pressure will be
\[p = \Phi\frac{F_{in}}{S_p} = 0.001854\textrm{ (Nm/(sccm s))} \frac{500\textrm{ (sccm)}}{1\textrm{ (m}^3\textrm{/s)}} = 0.927\textrm{ (Pa)}\]
2.2 Numerical Constraints
In Direct Simulation Monte Carlo (DSMC) simulation, the transport of particles along their trajectories can be considered as a grid less simulation method. The main function of the simulation grid in space is to resolve the collision dynamics, namely the dimension of the grid cells define the neighbourhood of particles which can collide with each other during a time step. Thus, in DSMC simulation the main criterion to select the cell spacing is the mean free path \(\lambda\).
In Particle-in-Cell Monte-Carlo (PIC-MC) plasma simulation, an additional function of the volume grid is to discretize the electric and magnetic field. The grid spacing should be appropriate to resolve gradients in the electric potential. This is most critical at the plasma sheath and in regions of high plasma density. The crucial criterion for cell spacing in plasma simulation is the Debye length \(\lambda_D\), which is a characteristic shielding length of potential fluctuations in the plasma.
2.2.1 Numerical constraints in Direct Simulation Monte Carlo (DSMC)
For a gas flow simulation, the set up of the simulation domain and the particle statistics requires to decide values for certain parameters, which are listed in the following. For simplicity we assume that all cells have a cubical shape. Then, the following parameters are relevant
- \(a\) = Cell dimension (m)
- \(V_c\) = Cell volume = \(a^3\)
- \(N_{\textrm{Real}}\) = Quotient between physical number of particles \(N\) and number of simulation particles \(N_S\)
- \(\delta t\) = Period of one time cycle.
The first step is to estimate the mean free path \(\lambda\) from the gas species and the expected pressure range.
The mean free path \(\lambda\) is defined as the mean travelling distance of a particle between two collisions. If a particle ensemble has a Maxwellian velocity distribution, it can be computed via
\[\lambda = \dfrac{1}{\sqrt{2}\,n\,\sigma} = \dfrac{k_\textrm{B}\,T}{\sqrt{2}\pi\,d^2\,p}\]{#eq:mean_free_path}
with the following parameters
- \(n\) = Density
- \(p\) = Pressure
- \(k_B\) = Boltzmann constant
- \(d\) = Effective collision diamater of the gas particle
- \(T\) = Temperature
- \(\sigma\) = Effective collision cross section
Eqn. ((eq:mean_free_path?)) shows, that \(\lambda\) is inversely proportional to the total pressure. From Pfeiffer-Vacuum / Mean free path the following numerical values are obtained for a few common gases at \(T\)=0 °C.
| Species | \(p\times\lambda\) (Pa mm) | Atomic diameter (nm) |
|---|---|---|
| Ar | 6.34 | 0.382 |
| H2 | 11.06 | 0.288 |
| N2 | 5.96 | 0.394 |
| O2 | 6.41 | 0.380 |
For temperatures \(T\) different than \(0\,^\circ C\) or \(273.15 K\), the mean free path can be obtained from Table (tbl:mfp?) by multiplying with \(T (K)/273.15\). The cell dimension \(a\) should be less than the mean free path to maintain proper collision statistics,
\[ a \le \lambda\]
Once, the cell dimension \(a\) is chosen, the maximum allowable timestep \(\delta t_{max}\) can be computed from the mean thermal velocity \(\overline{c}\) of the gas species,
\[\overline{c} = \sqrt{\frac{8 kT}{m\pi}}\]{#eq:thermal_velocity} \[\delta t_{max} = \frac{a}{\overline{c}}\]{#eq:max_time_step}
Finally, the physical number \(N_c\) of particles in a cell with volume \(V_c\) follows from the ideal gas equation,
\[N_c = \frac{p V_c}{k T}\]{#eq:particle_number_in_cell}
The number \(N_S\) of simulated particles is usually much lower than the physical number of particles. It can be chosen as a compromise between statistical accuracy and computational speed. A good range for \(N_S\) is from 10 till 100 or more particles in regions of maximum density. In regions, where almost no collision is to be expected, \(N_S\) can be also chosen as less than 10 or even less than 2. If an average particle number per cell \(N_c\) is obtained from Eqn. ((eq:particle_number_in_cell?)), and \(N_S\) is the desired mean simulation particle number per cell, the statistical weight factor can be obtained via
\[N_{\textrm{Real}} = \frac{N_c}{N_S}\]{#eq:nreal}
2.2.2 Numerical example for DSMC
In this numerical example, we are assuming to have Argon gas at a temperature of 300 K and a total pressure of \(0.5\,\textrm{Pa}\). From Table (tbl:mfp?) and Eqn. ((eq:mean_free_path?)) follows a mean free path of
\[\lambda_{\textrm{Ar, 300 K}} = 6.34\,(\textrm{Pa mm})\times\frac{300 K}{273.15 K\times 0.5 Pa} = 13.94\,\textrm{mm}\]
That means that the maximal cell spacing can be almost 14 mm; in order to be on the safe side and have a convenient factor between cells and space, we chose \(a = 10\,\textrm{mm}\), leading to a cell volume of \(V_c = a^3 = 10^{-6}\,\textrm{m}^3\). From Eqn. ((eq:thermal_velocity?)) we get \(\overline{c} = 398.5\,\textrm{m/s}\) as mean thermal velocity, which - via Eqn. ((eq:max_time_step?)) - defines an upper limit of the time step of \(\delta t_{max} = 2.5\times 10^{-5}\,\textrm{s}\).
For the particle scaling factor \(N_{\textrm{Real}}\) we consider that we would like to have a mean simulation particle number per cell of \(N_S = 20\). From Eqn. ((eq:particle_number_in_cell?)) the physical particle number per cell computes to \(N_c = 1.21\times 10^{14}\). Via Eqn. ((eq:nreal?)), this translates to \(N_{\textrm{Real}} = 6.05\times 10^{12}\).
2.2.3 Numerical constraints in Particle-in-Cell Monte-Carlo (PIC-MC) simulation
2.2.3.1 Cell spacing
One limitation for the maximum time step width is given due to the implemented Monte Carlo algorithm. According to their velocities particles must stay within a grid cell for at least on time step. Otherwise the collision probabilities are not evaluated correctly, i.e. a cell hopping occurs. Hence, the product of time step and particle velocity must not exeed the cell spacing,
\[\Delta t \times v < \Delta s\]{#eq:constraint_cellspacing}
The velocity of charged particles can be estimated from the maximum voltage in the simulation setup. If neglecting the energy loss due to inelastic collisions, the voltage potential is applied as kinetic energy to the charged particle:
\[\frac{m\,v^2}{2\,q} = E_\textrm{kin} (\textrm{eV}) = U_\textrm{max} (\textrm{V}) \Rightarrow v = \sqrt{\frac{2\,U\,q}{m}} \left[\dfrac{\textrm{m}}{\textrm{s}}\right]\]{#eq:constraint_charge_velocity}
with \(q = 1.60211 \times 10^-19\) (As). The table below lists electron velocities for various energies and the accordant distance covered at a time step width of \(\delta t=10^{-11}\) (s):
| Energy (eV) | \(v_{\textrm{Electron}}\) (m/s) | \(v_{\textrm{Electron}}\delta t\) (\(\mu\)m) |
|---|---|---|
| 100 | \(5.932 \times 10^6\) | 59.32 |
| 200 | \(8.389 \times 10^6\) | 83.89 |
| 300 | \(1.027 \times 10^7\) | 102.7 |
| 400 | \(1.186 \times 10^7\) | 118.6 |
| 500 | \(1.326 \times 10^7\) | 132.6 |
2.2.3.2 Collision frequency
According to the Wikipedia1 the collision frequency \(nu\) can be descibed as the rate of collisions between two species in an given volume and time. Regarding both species \(A\) and \(B\) as hard spheres, \(nu\) is expressed as
\[\nu = n_A n_B \sigma_{AB} \sqrt{\frac{8 k_B T}{\mu_{AB}\pi}}\,(m^{-3} s^{-1})\]{#eq:collision_frequency}
where
- \(n_A\,(m^{-3})\) is the number density of species \(A\)
- \(n_B\,(m^{-3})\) is the number density of species \(B\)
- \(\sigma_{AB}\,(m^2)\) is the collision cross section of \(A\) and \(B\)
- \(k_B\, (m^2\,kg\,s^{-2}\,K^{-1})\) is the Boltzmann’s constant
- \(T\,(K)\) is the temperature
- \(\mu_{AB}\,(kg)\) is the reduced mass of A and B
Since we are interested in the lower bound of the time step, only the highest cross section is of interest which is usually the reaction of the main gas species with itself.
2.2.3.3 Electron collision frequency
The collision frequency for neutrals in an ideal gas can be estimated from
\[\nu = N\,\pi d^2\sqrt{\frac{8 k_B T}{m \pi}}\]{#eq:collision_frequency_2}
Whereas \(N\) is the number density, \(d\) the effective atom radius, \(k_B\) the Boltzmann constant, \(T\) the gas temperature and \(m\) the molecular mass. Transfered to the electron collision frequency in a partly ionized plasma one could use the above estimation with:
- \(\pi d^2 \rightarrow \sigma\) = the electron-neutral collision cross section with the primary gas species
- \(T \rightarrow T_e\) = the electron temperature whereas 1 eV = 11604.5 K
- \(m \rightarrow m_e\) = the electron rest mass of \(9.1091 \times 10^{-31}\) kg
Thus, for a H2-plasma with TH2 = 500 K, Te = 5 eV and an approximated \(\sigma\) = 10-19 m2 one gets:
- \(\lambda=1.0838\times 10^{10}\,\textrm{Hz at }P_{H_2} = 500\,\textrm{Pa}\)
- \(\lambda=2.1677\times 10^{10}\,\textrm{Hz at }P_{H_2} = 1000\,\textrm{Pa}\)
- \(\lambda=4.3355\times 10^{10}\,\textrm{Hz at }P_{H_2} = 2000\,\textrm{Pa}\)
For a valid simulation, time step width must be well below the reciprocal of the collision frequency.
2.2.3.4 Plasma frequency
The plasma frequency \(\omega_p\) is the angular frequency of the electron oscillations around the ions. It depends only on electron mass and density:
\[\omega_p = \sqrt{\frac{n e^2}{\epsilon_0 m_e}}\]{#eq:omega_p}
- \(n\) = Electron density
- \(e\) = Electron charge (\(1.6021\times 10^{-19}\) As)
- \(\epsilon_0\) = Dielectric permittivity (\(8.8542\times 10^{-12}\) F/m)
- \(m_e\) = Electron mass (\(9.1091\times 10^{-31}\) kg)
In order to properly resolve the plasma oscillations, the electron time step should be well below the respective oscillation period e.g., \(\delta t < 0.1 \omega_p\), as can be estimated from the following table:
| Electron density [m-3] | Plasma frequency [s-1] | Oscillation period [s] |
|---|---|---|
| 1015 | \(1.78\times 10^{9}\) | \(5.605\times 10^{-10}\) |
| 1017 | \(1.78\times 10^{10}\) | \(5.605\times 10^{-11}\) |
| 1019 | \(1.78\times 10^{11}\) | \(5.605\times 10^{-12}\) |
2.2.3.5 Debye length
The Debye length \(L_D\) describes the electrical shielding capability of the plasma. The potential difference induced by a local excess charge will drop to \(1/e\) of the original potential at the distance of \(L_D\). For electrons, the Debye length is given by:
\[L_D = \sqrt{\frac{\epsilon_0 k_B T_e}{n_e e^2}} \simeq 69.01\times\sqrt{\frac{T_e}{n_e}} \simeq 6070\times\sqrt{\frac{E (\textrm{eV})}{n_e}}\]
Here, \(\epsilon_0\) is the vacuum permittivity, \(k_B\) the Boltzmann constant, \(T_e\) the electron temperature, \(n_e\) the electron density and \(e\) the electron charge.
In order to properly resolve the electric potential distribution in the simulation grid, the cell size has to in the same order of magnitude as the Debye length. From (Langdon 1970) follows, that the cell spacing shall be less than \(\pi L_D\). In (Tskhakaya et al. 2007) a constraint of:
\[\delta_x \le 3.4 L_D\]
is suggested. This is what we also adopted in our constraint check message for the Debye length on plasma simulation startup. If this constraint is broken, artificial numerical oscillations will take over leading to “artificial heating,” i.e. more energy will be gained in the plasma than actually put into the system via the electrodes, and the simulation will become unstable.
Our simulation tool cannot predict the plasma density of any given simulation case. Therefore, we give some estimations for typical cases:
- We assume 5 eV for electrons as this is a very typical electron temperature in magnetron sputtering discharges.
- A plasma density of 1017/m³ corresponds to an experimentally realistic density (still with moderate power density, e.g. 50-100 W for a 3 inch cathode).
- A plasma density of less than 1015/m3 is what we often have in simulation (especially 3D) as feasible compromise between realistic power density and computation time.
As an example, for \(n_e = 10^15 m^{-3}\) and \(T_e = 5 eV\), the constraint \(3.4 L_D\) is computed to 1.459 mm.
If the simulation output shows “Failure” at the Debye length check this is merely an informative message based on the assumed plasma density of 1015/m³ or 1017/m³ and electron temperature of 5 eV. If the actual simulation setup is different from that it may be still numerically valid. If in doubt it helps to check if two simulation runs with slightly changed cell spacing yield the same overall results.
2.2.3.6 Gyrokinetics
The implemented leap-frog algorithm from Boris is very robust at comparatively small computation costs. Nevertheless if the chosen time step witdh is too large, gyrokinetic trajectories could not be resolved sufficiently as seen in the pictures below. For a proper estimation use the following equation:
\[R_{\textrm{Larmor}} = \frac{m_e\left|\vec{v}\right|}{q_e\left|\vec{B}\right|}\]{#eq:rlarmor}
with
- \(m_e = 9.1091\times 10^{-31}\) kg
- \(q_e = 1.6021\times 10^{-19}\) As
Eqn. ((eq:rlarmor?)) yields the path radius of an electron at constant velocity \(v\) perpendicular to a homogenous magnetic field \(B\). We still lack informations on how the time step related granularity is influencing the plasma simulation and the results respectively. However, for a proper simulation of gyrokinetic plasmas it should not exeed a certain limit. Apparant from the pictures below, at magnetic field strengths around 100 mT and electron velocities around \(5\times 10^6\) m/s, the time step for electrons should not exeed 10-10 s. These values are commonly valid for magnetron discharges in PVD sputtering processes, on which the PICMC simulation environment is focused on.
| Time Step = 10-11 [s] | Time step = 10-10 [s] |
|---|---|
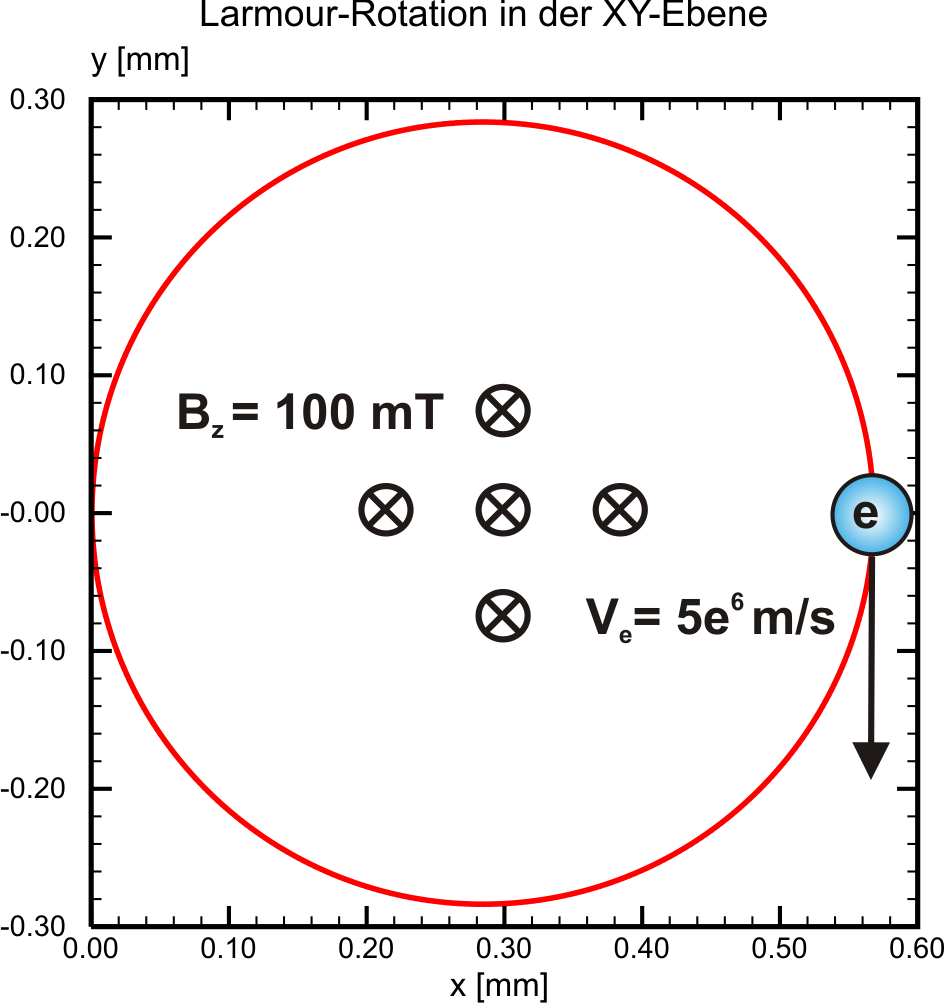 |
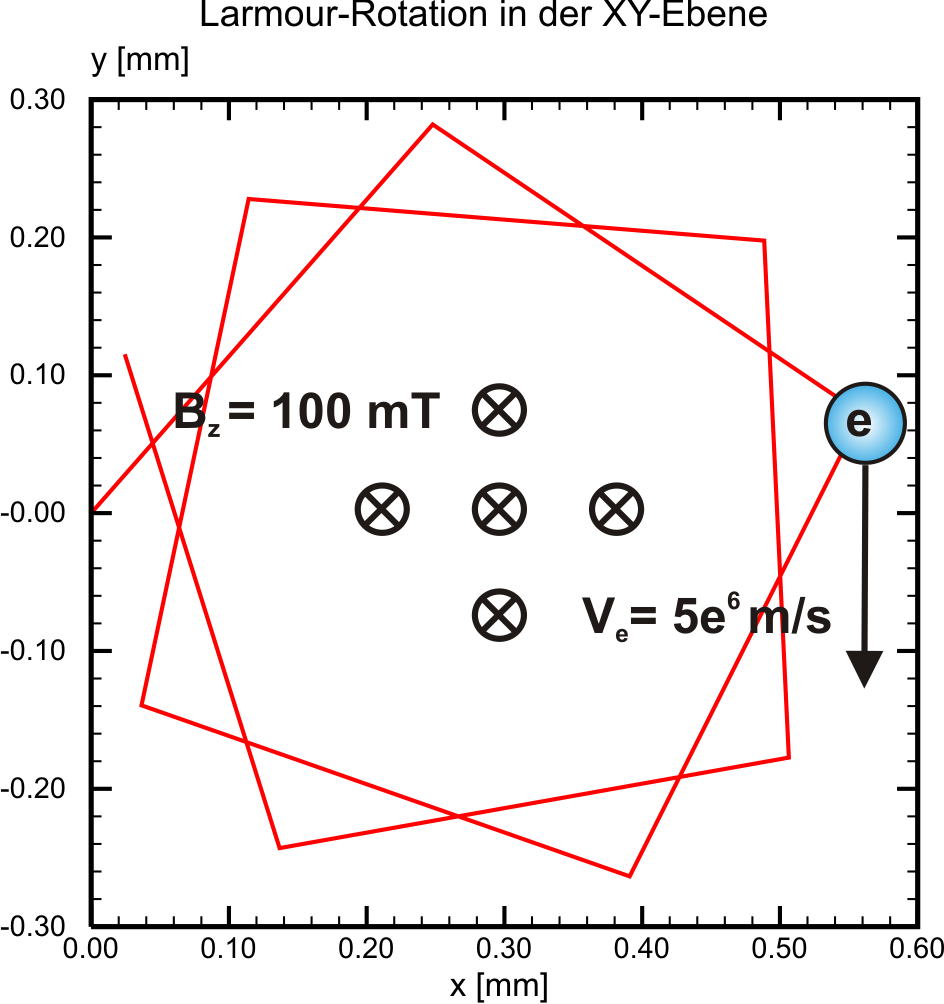 |
2.2.3.7 Isotropic vs. anisotropic cell spacing
Within the Particle-in-Cell (PIC) algorithm charged particles are mapped on the cell nodes by a weighting scheme. Then, in a successive computation step the Poisson Equation of the electric field can be solved consistently to the weighted charge distribution. The PIC weighting scheme in general delocalized a point charge to a finite sized space charge with an appropriate shape function. The charge on a certain node is then given by the fraction of the space charge within the cell volume.
In a homogenous grid the particle shape is equivalent to the cell spacing at every point. Thus, for a bilinear (trilinear) weighting scheme, the charge on a certain cell node can be described as the convolution of two square pulses over time:
\[Q_{Node}(t) = f_{Charge}(x,t)f_{Node}(x) = \int dx\, \Pi_{\Delta x}(x-v_x t)\Pi_{\Delta x}\]
The resulting plot for this mathematical operation can be seen below. Now if the particle's speed \(v_x\) is increased or the cell width \(\Delta x\) is decreased, the variation of \(Q(x,t)\) over time increases:
\[\left.\frac{Q(t)}{dt}\right|_{(v_x, \Delta x)} < \left.\frac{Q(t)}{dt}\right|_{2v_x, \Delta x}\,\,\textrm{and}\,\,\left.\frac{Q(t)}{dt}\right|_{(v_x, 2 \Delta x)} < \left.\frac{Q(t)}{dt}\right|_{v_x, \Delta x}\]
If the charge on a nodes varies over time so does the electric field resulting from the solution of the poisson equation:
\[\frac{Q(t)}{dt}\approx \frac{E(t)}{dt}\]
2.3 Collision routine
In order to treat the collision dynamics in proper resolution, the simulation volume is divided into simulation cells, whereof the cell spacing \(\delta x\) is less than the mean free path \(\lambda\). In these cells, the collision is treated with a statistical approach, which is called no time counter (NTC) - method. This method rather estimates the number of collisions in a simulation cell per time step instead of checking all possible particle trajectory intersections. The latter is quite time consuming and would scale with the square of the particle number.
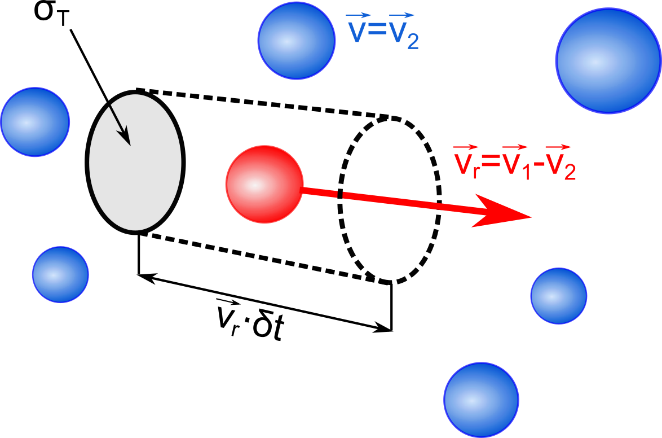
The estimation on the number of collisions is based on a model shown in Figure (fig:collision_sketch?). Let us assume we have a particle class, whereof each particle has a velocity \(v_2\) and let’s assume an inertial system, where \(v_2=0\). For a test particle with velocity \(v_1\), its cross section \(\sigma_T\) for collisions with particles of the class \(v_2\) can be considered as a circular area. If we multiply this area with the test particle’s trajectory during time step \(\delta t\), a cylindrical volume results. This volume is now put in ratio with the cell volume \(V_c\), which yields the collision probability
\[p_{12} = \frac{\sigma_T v_r \delta t}{V_c}\] {#eq:collision_1}
Here, \(v_r = |\vec{v}_1-\vec{v_2}|\) is the relative velocity between two potential collision partners, and \(\sigma_T\) is their total cross section. Equation ((eq:collision_1?)) says that the collision probability basically is proportional to the product \(\sigma_T v_r\). In general, \(\sigma_T\) depends on the relative velocity and other parameters. For a good initial estimate of the expected number of collisions, it is useful to take the maximum possible product of cross section and relative velocity, \(<\sigma_T v_r>_{max}\), which can be obtained from the energy-dependent cross section curve. Based on this, the maximum possible collision probability is
\[p_{12.max} = \frac{<\sigma_T v_r>_{max} \delta t}{V_c}\] {#eq:collision_2}
For two particle species 1, 2 with particle numbers of \(N_1, N_2\) per cell and a statistical weight factor of \(N_R\), the maximal expected number of collisions becomes
\[N_{\textrm{preselect}} = \frac{N_R N_1 N_R N_2}{N_R} p_{12.max} = N_R N_1 N_2 p_{12.max}\] {#eq:collision_3}
In the NTC method, a number of \(N_{\textrm{preselect}}\) pairs of collision partners is randomly selected from the particles within a cell. For each pair, their actual value of the product \(\sigma_T v_r\) divided by \(<\sigma_T v_r>_{max}\) is their relative collision probability. Based on that, the collision takes place with the selected particles, if the following random experiment succeeds:
\[r\# < \frac{\sigma_T v_r}{<\sigma_T v_r>_{max}} \]{#eq:collision_4}
Here, \(r\#\) is a random number between 0 and 1. The situation gets a bit more complicated in case of two collision species 1,2 and a reaction product 3 with different statistical weights \(N_{R1}, N_{R2}, N_{R3}\). In this case, the number of pre-selected collision pairs is computed via
\[N_{\textrm{preselect}} = \frac{N_{R1} N_1 N_{R2} N_2}{\min(N_{R1}, N_{R2}, N_{R3})}\times p_{12.max}\] {#eq:collision_5}
Note that now, the collision partner or reaction product with the least statistical weight is determining the number of to be preselected collision pairs. The decision, whether a collision for a randomly chosen pair actually takes place is again made via Equation ((eq:collision_4?)). After the collision it still has to be considered that the collision partners and reaction products all have different weight factors. Therefore, for each species \(i\) a post-collision probability \(w_i\) decides, whether the collision actually takes effect or not:
\[w_i = \frac{\min(N_{R1}, N_{R2}, N_{R3})}{N_{Ri}}\] {#eq:collision_6}
Example: Let Ar have a statistical weight of \(N_{R.Ar} = 10^{10}\) and electrons and ions each have \(N_{R.e}, N_{R.i} = 10^5\). After an ionization collision
\[\textrm{Ar}+e^- \rightarrow \textrm{Ar}^+ + 2e^-\] {#eq:ar_ionization}
equation ((eq:collision_6?)) yields post-collision probabilities for electrons and ions of 1.0 and for Argon \(w_{Ar} = 10^{-5}\). Thus, in each performed ionization collision, an electron and ion is actually created but the Ar neutral with the much heigher statistical weight is deleted in only 1 out of 100000 cases. The same principle holds for the modification of the collision partner’s velocities.
There is the additional complication that some of the species might be frozen. In this case, equation ((eq:collision_5?)) is modified as follows.
\[N_{\textrm{preselect}} = \frac{N_{R1} N_1 N_{R2} N_2}{\min(\textrm{statistical weights of all non-frozen species})}\times p_{12.max}\] {#eq:collision_7}
The post-collision probability is analogously modified to
\[w_i = \frac{\min(\textrm{statistical weights of all non-frozen species})}{N_{Ri}}\] {#eq:collision_8}
In case of frozen species they do not exist in form of particles but merely with time-averaged values for the particle density \(<n>\), their cartesian velocity components \(<v_x>, <v_y>, <v_z>\) and their square velocity \(<v^2>\). From these values, test particles for the collision can be generated. First, their kinetic temperature \(T\) can be computed from the velocity averages by
\[T = \frac{m}{3k_B}\left\{<v^2>-<v>^2\right\},\,\textrm{with }<v>=\sqrt{<v_x>^2+<v_y>^2+<v_z>^2}\] {#eq:collision_9}
Here, \(m\) is the atomic mass of the frozen species, and \(k_B\) is the Boltzmann constant. From the temperature and mass, velocity components can be randomly chosen according to the following method
\[v = \sqrt{-\frac{2k_B T \ln(r\#)}{m}}, \phi=2\pi r\#, v_1=v\sin(\phi), v_2=v\cos(\phi)\] {#eq:collision_10}
Unfortunately, equation ((eq:collision_10?)) yields only two velocity components \(v_1, v_2\) while a real particle needs three. Thus, ((eq:collision_10?)) is executed two times, and three velocity are selected out of the four.